7月18日の数学検定準1級の受験を目指し、なんとか合格までの道筋を作っていきたいと思います。
受験までの流れ
- 中学数学の復習と演習
- 過去問の流し読みとレベル感の把握
- 白チャートの通読
- 白チャートの演習
- 過去問演習
現在はこの流れで考えています。
1. 中学数学の復習と演習
まず高校数学の範囲に入る前に、中学数学を復習しました。
これでも大学は理系コースだったので、「中学数学ぐらいはできるだろう!」という謎の自信はありましたが、自分の実力は過信せず、中学生まで戻って復習することにしました。
というのも数学は英語と同じように、積み上げ型の科目です。前の単元を理解できていないと、新しいことを学習しても効果は薄くなってしまいます。
例えば
中学で習う二次関数を理解していないと、高校の発展形の理解は難しい
中学で習う三角形の性質を理解していないと、高校で習う三角比や図形の性質理解は難しい
などが挙げられます。
そこでまずは下のような本を使い、短期間で集中的に中学生で習う数学をおさらいしました。
さらに薄い問題集を一冊購入し、こちらも解いてみました。
正直、「中学数学なら余裕だろう」と思っていましたが、これが解いてみるとなかなか発展問題に苦戦。
ここでの目的は、中学で習った範囲を思い出すことなので、発展問題までを完璧に解けるようにする必要はありません。
目安として全体の7-8割を理解できれば良しとして、次へ進むこととしました。
2. 過去問の流し読みとレベル感の把握
中学数学を1週間程度でサラッとおさらいしたら、次は過去問に目を通し、出題され問題のレベル感を把握していきます。
「いきなり過去問なんて解けるわけない!」と思われる方も多いでしょう。もちろん解けません。ここでの目的は解くことではなく、レベル感の把握にあります。
試験の目的は、合格点に達することです。なのでこれから半年間で、最低限どのレベルまで到達するかを把握しておく必要があります。
これは資格試験に限らず、受験勉強も含めてどんな試験でも共通です。受験の場合は共通試験の点数で、自分のレベルをだいたい測ることができます。
自分の現在のレベルと、目指すべきギャップを明らかにした上で、初めて戦略が立てられるようになります。
ここでの過去問の流し読みはあまり時間をかけず、サラッと流す程度で済ませます。「あと半年でこれらの問題を解けるようにならないといけないのね」と確認し、次へと進みます。
3. 白チャートの演習
白チャートを選んだ理由
中学数学の復習サラッと完了し、過去問で到達レベルを確認したら、いよいよ問題演習へと移ります。
僕の場合は『白チャート』と呼ばれる網羅型の参考書を使うことに決めました。
一応白チャートを選んだ理由を簡単に。それは現在の自分のレベルに一番適していると判断したらからです。
大学受験の数学参考書で、おそらく一番有名なチャートシリーズ。表紙の色ごとにレベルが別れていて、難しい方から赤・青・黄・白となっています。
入試では一般的に、青か黄色が推奨されています。しかし今回は一番簡単で解説が詳しい白を選びました。
勉強テキストを選ぶ上で、選択肢が豊富にある場合自分のレベルにあった適切なものを選ぶことが重要だと思います。これは途中で挫折し、チャレンジをやめてしまうのを防ぐためです。
また過去問を見たり、過去に受験した人の体験談を読む限り、数検自体は準1級といえど、そこまで難しいレベルの計算が要求されていません。
そこでいきなり難しい参考書にチャレンジするのではなく、今の自分のレベルに適したテキストを選ぶことにしました。
白チャートのオススメの使い方についてはこちらをご覧ください。
なお、本当に知識ゼロから数学にチャレンジする場合、まずは講義形式の参考書から勉強することが推奨されています。あくまでチャート式は問題演習用として使います。
これでも僕は大学で理数系だったため、一応高校のときに数学3までを履修しました (ほとんど忘れましたが…)。なのでいきなり白チャートから入りましたが、本当に数学が苦手、または初学者の方は、マセマ出版社の『初めから始める』シリーズなどが良いかもしれません。
白チャートの進め方
まずは数学Ⅰ〜Ⅲまで1回通読します。
ここでは問題を解いたり、いきなり暗記せず、全体像を確認します。
僕は高校で数学Ⅲまで履修しましたふぁ、今の数学とはだいぶカリキュラムが変わっています。「データ分析 (統計) が追加されたな」「三角比とか三角関数、懐かしいなぁ」といったかんじで、ページをパラパラとめくり、これから勉強していく範囲を確認しました。
白チャートの例題演習
通読を終えて全体像を把握したら、いよいよ演習です。
ここでは例題を解き進め、練習問題などには手をつけません。
まずは試験日の1ヶ月前までに、数Ⅰ〜数Ⅲの例題をすべて解けるようにすることが目標です。
実際に解いたり解かなかったり
白チャートでは、数Ⅲの範囲まで例題数を合計すると、約800問あります。
[参考]>>>【例題だけでいい!?】白チャートの問題数、レベル、使い方を徹底解説これを一からすべて丁寧に解いていては、とてもじゃないですが時間が足りません。
そこで僕の進め方としては
1回目) 解説を読みながらノートに書き写す
チャート式に記載されている解法を、実際にノートに書き出します。
このとき、答案を書く上で欠けてはならない要素 (xは整数, sinθ>0とか) を抑えながら、書き写すことがポイントです。
解法を読んできちんと理解できていればOK。理解できない場合、Youtubeなどの数学講義を見て、理解できるよう努めます。
僕が受験生だった頃、ユークリッドの互除法やn進数は試験範囲に含まれていませんでした。
初見でこれらの問題を、チャート式の解説だけ読んで理解、いきなり問題を解くのは正直無理がありました。そこでYoutubeの解説などをフルに活用し、理解を深めました。
これだけわかりやすい講義が無料で受けられて…いい時代だと思います。
2回目) 問題を読んで解答
2回目以降は自力で解答をノートに書き出し、解いていきます。
ここでの目的は、「解ける問題と解けない問題を仕訳すること」にあります。
1周目で問題の解法は理解できているはずなので、2回目に解く時点では、問題を解くための知識は持ち合わせているはずです。
しかし数学においては問題を理解できることと解けることは意味が異なります。
ここでは解けるはずの問題にチャレンジし、自分が実際にその問題を理解して解けるのか、それとも理解できていると思いこんでいるだけなのか? を明らかにします。
解けた場合はOK、解けなかった場合はもう一度解き方を確認し、再度理解するようにします。
3回目以降) 解けなかった問題は解けるまで、解けた問題は解き方を忘れないように
2周目で問題を実際に解けるか解けないかを仕訳したあとは、自分のペースで学習を進めます。
2周目、3周目と進める中で、徐々に理解を深めていきます。
得意な問題は何度も解く必要はありませんが、解き方を忘れないように定期的に確認しておくことは必要です。
中にはなかなか解けるようにならない問題もあります。そういう問題は解法暗記でも良いので、一回は自力で解答を書けるようにし、あまり立ち止まらずに先へ進むようにしています。
というのも、数学は先に進んでいるうちに突然理解できるようになるケースもあるからです。
また準1級は数Ⅲまでと範囲が広く、細かいところで立ち止まっているとなかなか先へ進めず、時間切れになってしまいます。
解法暗記は本質的な理解とは言えないかもしれませんが、まずは全ての例題を1周解けるようにすることに重きをおいています。
Ankiの活用
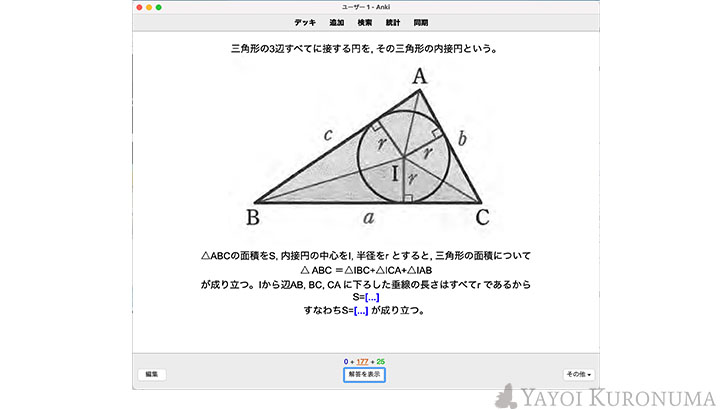
以前サイトで紹介したAnkiというフラッシュカードアプリを活用しています。
Ankiは語学の単語学習のようなシーンでよく使われておりますが、あまり数学で使われている事例は目にしません。
しかし例題と解答を登録しておけば、プログラム通りに復習スケジュールを作ってくれるので、とても便利です。
あらかじめ例題と解答を登録しておけば、一定頻度で問題を出題してくれ、その都度確認することができます。またよく間違える苦手な問題は、頻繁に出題してくれるので、解法が身体に染み込むまで徹底して反復学習ができます。
デフォルトの復習頻度 (1分、1時間 …) だと使い勝手が悪かったので、復習頻度は1日後、2日後、3日後になるように設定を変えて使っています。
Ankiの効率のよい復習頻度の設定は、以前ご紹介した『最新研究からわかる 学習効率の高め方 Anki巻』でより詳しく知れるので、参考にしてください。
[リンク]>>>最新研究からわかる 学習効率の高め方 Anki巻過去問演習
試験1ヶ月前になったら、最後は過去問演習で問題の傾向を把握し対策していきます。
試験の場合は何よりも過去問演習が大切です。最後の1ヶ月は理想は3周、最低2周は過去問を解けるよう、スケジュールを調整する必要があります。
そのためにも、1ヶ月前までには全単元を学習し終えるできるようペース配分して学習していこうと思います。
まとめ
- 中学数学の復習と演習
- 過去問の流し読みとレベル感の把握
- 白チャートの通読
- 白チャートの演習
- 過去問演習
とここまで「これだけやれば、数検定準1級といえども合格できるでしょう」という道筋を立ててきました。
しかし計画は立てることではなく、実行することが大切です。当たり前ですが…。
7月18日の試験に向けて、着実に勉強していこうと思います。














コメントを残す